El movimiento circular es el que recorre una partícula o cuerpo por una circunferencia. Este movimiento tiene un eje y todos los puntos por los que pasa la partícula se encuentran a una distancia constante (r) del eje.
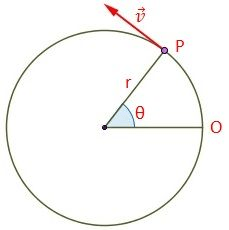
La velocidad angular es la derivada del ángulo que forma el radio con un eje en el plano del movimiento en función del tiempo:
\omega=\dfrac{d\theta}{dt}En el caso de que la velocidad angular sea constante (Movimiento Circular Uniforme), se puede integrar esta expresión para obtener la ecuación que nos da la relación entre la velocidad angular y el ángulo recorrido:
\theta=\theta_0+ \omega\cdot t
Donde:
- \theta_0 es el ángulo en el instante inicial
En el caso de que la velocidad no sea constante, definimos la aceleración angular como la derivada de dicha velocidad angular:
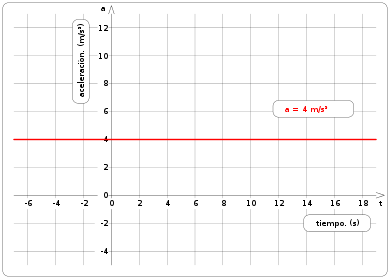
\alpha=\dfrac{d\omega}{dt}Cuando dicha aceleración es constante (Movimiento Circular Uniformemente Acelerado), se puede integrar esta expresión para obtener las ecuaciones del movimiento:
\omega=\omega_0+\alpha\cdot t
\theta=\theta_0+\omega_0\cdot t+\dfrac{1}{2}\cdot\alpha\cdot t^2Donde:
- \theta_0 es el ángulo en el instante inicial
- \omega_0 es la velocidad angular en el instante inicial
Una partícula situada a una distancia R del eje del movimiento, se moverá con una velocidad lineal que se puede obtener a partir de la siguiente expresión:
v=\omega\cdot R


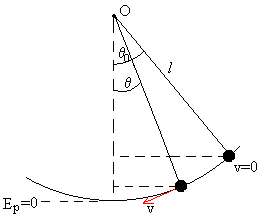
Una idea sobre “Movimiento circular”