El movimiento armónico simple es un movimiento periódico de vaivén, en el que un cuerpo oscila de un lado al otro de su posición de equilibrio, en una dirección determinada, y en intervalos iguales de tiempo. Por ejemplo, es el caso de un cuerpo colgado de un muelle oscilando arriba y abajo. El objeto oscila alrededor de la posición de equilibrio cuando se le separa de ella y se le deja en libertad. En este caso el cuerpo sube y baja.
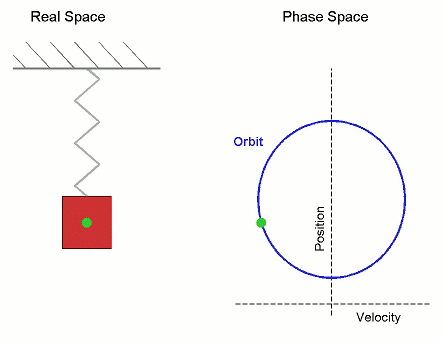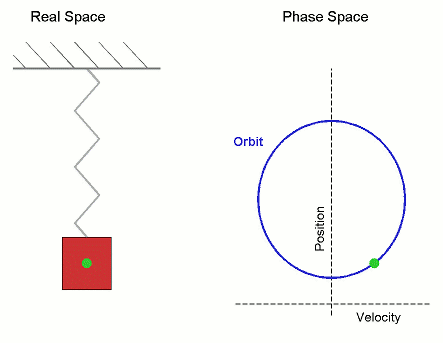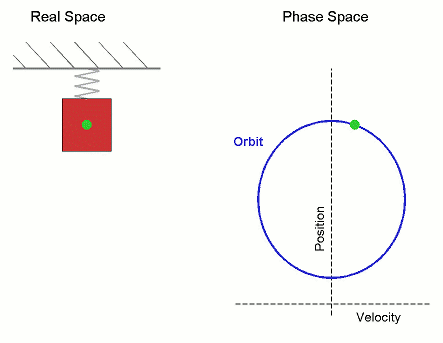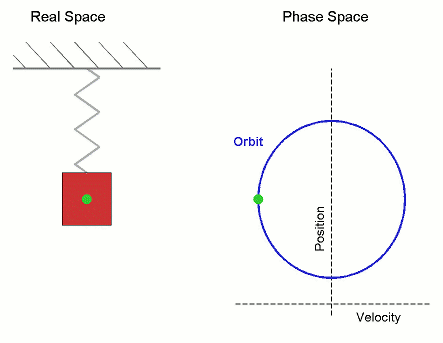
Es también, el movimiento que realiza cada uno de los puntos de la cuerda de una guitarra cuando esta entra en vibración; pero, pongamos atención, no es el movimiento de la cuerda, sino el movimiento individual de cada uno de los puntos que podemos definir en la cuerda. El movimiento de la cuerda, un movimiento ondulatorio, es el resultado del movimiento global y simultáneo de todos los puntos de la cuerda.
Posición (negro), velocidad (verde) y aceleración (rojo) de un oscilador armónico simple.
Respecto a su posición de equilibrio. En un desplazamiento a lo largo del eje Ox, tomando el origen O en la posición de equilibrio, esta fuerza es tal que F_{x}=-kx donde k es una constante positiva y x es la elongación. El signo negativo indica que en todo momento la fuerza que actúa sobre la partícula está dirigida hacía la posición de equilibrio; esto es, en dirección contraria a su elongación (la «atrae» hacia la posición de equilibrio).
Aplicando la segunda ley de Newton, el movimiento armónico simple se define entonces en una dimensión mediante la ecuación diferencial:
m\cdot\dfrac{d^2x}{dt^2}=-k\cdot xLa solución de esta ecuación diferencial es:
x(t)=A\cdot cos(\omega\cdot t+\phi)
Donde:
- x es la elongación o desplazamiento respecto al punto de equilibrio
- A es la amplitud del movimiento
- \omega es la frecuencia angular
- t es el tiempo
- \phi es la fase (o desfase) inicial e indica el estado de oscilación en el instante t=0
A partir de esta ecuación, podemos obtener las expresiones de la velocidad y de la aceleración en cada instante t:
v(t)=-A\cdot \omega\cdot sen(\omega\cdot t+\phi)
a(t)=-A\cdot \omega^2\cdot cos(\omega\cdot t+\phi)=-A\cdot \omega^2\cdot x(t)
El péndulo simple
El movimiento que describe el péndulo simple es un caso particular de este movimiento armónico simple. Un péndulo simple se define como una partícula de masa m suspendida del punto O por un hilo inextensible de longitud l y de masa despreciable. Si la partícula se desplaza a una posición \theta_0 (ángulo que hace el hilo con la vertical) y luego se suelta, el péndulo comienza a oscilar.

El péndulo describe una trayectoria circular, un arco de circunferencia de radio l, que es la longitud del hilo. Las fuerzas que actúan sobre la partícula de masa m son dos:
- El peso: m\cdot g
- La tensión T del hilo
Ecuación del movimiento en la dirección radial
La aceleración de la partícula es a_n=\dfrac{v^2}{l}, dirigida radialmente hacia el centro de su trayectoria circular.
La segunda ley de Newton se puede escribir como:
m\cdot a_n=T-m\cdot g\cdot cos(\theta)
Conocido el valor de la velocidad v en la posición angular \theta, podemos determinar la tensión T del hilo.
La tensión T es máxima cuando el péndulo pasa por la posición de equilibrio y es mínimo en los extremos de su trayectoria, cuando la velocidad es cero.
Principio de conservación de la energía
En la posición \theta=\theta_0 el péndulo solamente tiene energía potencial, que se transforma en energía cinética cuando el péndulo pasa por la posición de equilibrio.
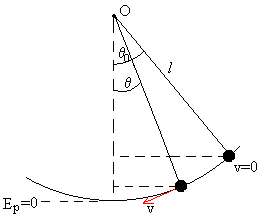
Comparemos las dos posiciones del péndulo:
En la posición extrema \theta=\theta_0 , la energía es solamente potencial:
E=mg(l-lcos\theta_0)
En la posición \theta, la energía del péndulo es cinética y potencial:
E=\dfrac{1}{2}mv^2+mg(l-lcos\theta)Como la energía se conserva, podemos igualar dichas energías, con lo que obtenemos:
v^2=2gl(cos\theta-cos\theta_0)
Y, por lo tanto, la tensión del hilo viene dada por:
T=mg(3cos\theta-2cos\theta_0)
La tensión de la cuerda no es constante, sino que varía con la posición angular \theta. Su valor máximo se alcanza cuando \theta=0, esto es, cuando pasa por la posición de equilibrio (la velocidad es máxima). Su valor mínimo se alcanza cuando \theta=\theta_0 (la velocidad es nula)