Composición de movimientos: Tiro parabólico

El tiro parabólico surge de la composición de dos movimientos:

• Un MRU horizontal con velocidad v_x
• Un MRUA vertical con velocidad inicial v_{0y} y aceleración a=g=-9,8m/s^2

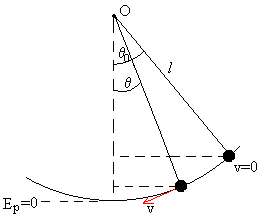
Este sería el esquema de un tiro parabólico de un proyectil lanzado desde una altura h con una velocidad inicial \vec{v}, que forma un ángulo \alpha con la horizontal:

Las componentes del vector velocidad inicial, \vec{v_0} están relacionadas con el ángulo \alpha_0 a través de su tangente:

tan(\alpha_0)=\dfrac{v_{0y}}{v_x}

Además, en cualquier momento, las componentes del vector velocidad son:

\vec{v_x}=v\cdot cos(\alpha)

\vec{v_y}=v\cdot sen(\alpha)

Y, por el teorema de Pitágoras:

v=\sqrt{v_x^2+v_y^2}

Ecuaciones del movimiento

En la dirección horizontal, el proyectil describe un MRU, por lo que la ecuación de su movimiento viene dada por:

x(t)=x_0+v_x\cdot t=0+v_0\cdot cos(\alpha_0)\cdot t=v_0\cdot cos(\alpha_0)\cdot t

En la dirección vertical, el proyectil describe un MRUA con a=g=-9,8m/s^2, por lo que la ecuación del movimiento vendrá dada por:

y(t)=y_0+v_{0y}\cdot t+\dfrac{1}{2}\cdot a \cdot t^2=h+v_0\cdot sen(\alpha_0)\cdot t-\dfrac{1}{2}g\cdot t^2

A menos que nos indiquen otra cosa, la altura inicial (h) será nula.

Utilizando estas fórmulas, se pueden obtener algunos datos interesantes:

Altura máxima

La altura máxima y_{max} se alcanza cuando la velocidad vertical se anula:

v_y(t)=v_0\cdot sen(\alpha_0)-gt=0

Despejando el tiempo t=\dfrac{v_0\cdot sen(\alpha_0)}{g} y sustituyendo en y(t):

y_{max}=h+\dfrac{v_0^2\cdot sen^2(\alpha_0)}{2g}